Warren Buffett’s extraordinary wealth didn’t come from advanced algorithms or refined buying and selling methods. As a substitute, the Oracle of Omaha constructed his $140+ billion fortune by persistently making use of easy mathematical ideas to funding choices.
Whereas Buffett famously said that advanced math isn’t vital for profitable investing, his wealth-building technique depends on elementary mathematical ideas that present a scientific framework for evaluating alternatives and managing danger.
The next seven mathematical guidelines exhibit how disciplined quantitative considering, utilized over a long time, can rework modest investments into extraordinary wealth. Let’s discover every one.
1. The Compound Curiosity Formulation
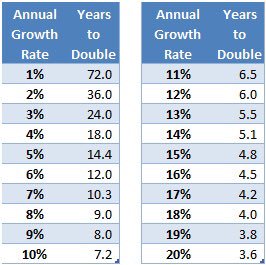
Buffett found the facility of compound curiosity early in life, understanding that point transforms modest investments into extraordinary wealth by means of the mathematical system A = P(1 + r/n)^nt. This equation demonstrates how the principal quantity, rate of interest, compounding frequency, and time create exponential progress. Buffett has referred to as compound curiosity the eighth marvel of the world, emphasizing that beginning early maximizes the time part within the equation.
The mathematical great thing about compounding lies in incomes returns not simply in your authentic funding, however on all beforehand collected beneficial properties. A $10,000 funding incomes 10% yearly turns into $11,000 after one yr, however the second yr’s 10% return applies to the total $11,000, creating $12,100.
Over a long time, this accelerating impact has grow to be dramatic, explaining Buffett’s choice for getting and holding high quality firms for prolonged durations fairly than frequent buying and selling. This precept applies to compounding capital beneficial properties and reinvested dividends, which Buffett has persistently optimized all through his profession.
2. The Loss Restoration Rule
Buffett’s well-known precept, “By no means lose cash,” stems from the mathematical asymmetry of losses and beneficial properties. When an funding loses 50% of its worth, it wants a 100% acquire to interrupt even. This mathematical actuality turns into extra extreme with bigger losses: a 75% decline requires a 300% acquire for restoration, whereas a 90% loss calls for a 900% acquire.
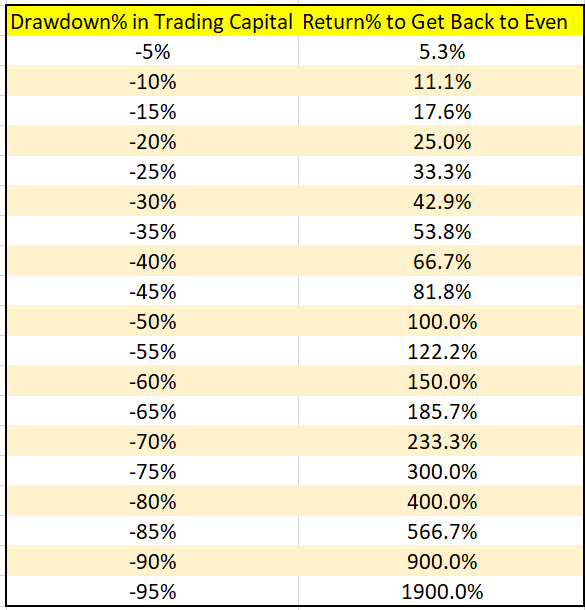
This mathematical drawback explains Buffett’s conservative strategy to danger administration. Fairly than chasing high-risk, high-reward alternatives, he focuses on preserving capital by investing in firms with predictable earnings and substantial aggressive benefits.
The arithmetic clearly present that avoiding important losses contributes extra to long-term wealth creation than often hitting dwelling runs whereas struggling substantial setbacks. This precept underlies his well-known investing guidelines: “Rule No. 1: By no means lose cash. Rule No. 2: Always remember rule No. 1.”
3. Discounted Money Circulation Evaluation
Buffett determines intrinsic worth by calculating the current worth of an organization’s future money flows utilizing discounted money circulation evaluation. The system IV = Σ(CFt / (1 + r)^t) represents the sum of all future money flows divided by one plus the low cost charge raised to the facility of durations. This mathematical strategy values firms primarily based on their skill to generate money for shareholders fairly than market sentiment or hypothesis.
Buffett defines “proprietor’s earnings” as web revenue plus depreciation and amortization, minus capital expenditures and extra necessities. This calculation offers a extra correct image of money obtainable to shareholders.
By evaluating this intrinsic worth to the present market value, Buffett identifies undervalued alternatives the place mathematical evaluation suggests the inventory trades under its elementary worth. This disciplined strategy transforms investing from hypothesis into a scientific analysis of what the enterprise is value primarily based on future projected earnings.
4. Alternative Price Optimization
Each funding choice includes alternative price – the return foregone by selecting one funding over alternate options. Buffett applies mathematical considering by consistently evaluating potential returns throughout completely different alternatives, even in unrelated industries. This optimization course of requires evaluating risk-adjusted returns to allocate capital to probably the most engaging alternatives.
Buffett’s strategy includes creating psychological hurdles that investments should exceed to be thought-about. When evaluating a possible inventory buy, he compares its anticipated returns to bonds, different shares, and maintaining money. This mathematical framework ensures capital flows towards alternatives providing one of the best risk-adjusted returns fairly than merely probably the most acquainted or handy choices.
The systematic comparability of alternate options throughout completely different asset courses has enabled Buffett to deploy capital the place it could actually persistently generate the best returns.
5. The Focus Rule
Buffett advocates concentrating investments in your finest concepts fairly than diversifying throughout many mediocre alternatives. His strategy includes itemizing potential investments, figuring out the highest 5 most tasty choices, and focusing solely on these whereas avoiding the temptation to pursue the remaining twenty. This mathematical strategy to portfolio development acknowledges that extreme diversification can dilute returns.
The arithmetic of focus work as a result of distinctive firms generate outsized returns that common performers can’t match. Whereas diversification reduces volatility, it limits upside potential while you genuinely imagine in superior alternatives.
Buffett’s concentrated strategy requires thorough evaluation however permits mathematical compounding to work in your finest concepts fairly than being diluted throughout quite a few common investments. His portfolio has traditionally been concentrated in his highest-conviction positions, enabling him to learn absolutely from his finest funding choices.
6. Return on Fairness Evaluation
Return on Fairness measures how effectively an organization generates income from shareholder fairness: ROE = Internet Revenue ÷ Shareholder Fairness. Buffett seeks firms with persistently excessive ROE, which signifies administration’s skill to create worth from invested capital. This mathematical metric reveals how successfully firms deploy shareholder cash to generate earnings.
Corporations with sustainable excessive ROE possess aggressive benefits that permit them to earn superior returns on invested capital. These companies typically require minimal extra funding to develop, permitting them to compound shareholder wealth effectively.
Buffett’s concentrate on ROE displays his mathematical understanding that companies producing excessive returns on fairness create extra worth than these requiring fixed capital infusions to take care of progress. This metric helps establish firms that may reinvest earnings at engaging charges, making a virtuous cycle of wealth creation.
7. Margin of Security Calculation
Buffett solely purchases shares once they commerce considerably under the calculated intrinsic worth, making a margin of security that’s expressed as intrinsic worth minus market value. This mathematical buffer protects towards analytical errors, unexpected circumstances, and market volatility. The bigger the margin, the better the safety towards everlasting capital loss.
This precept, inherited from Benjamin Graham, acknowledges that funding evaluation includes estimates and assumptions which will show incorrect. Buffett reduces the chance of great losses whereas growing potential returns by requiring a considerable mathematical cushion between intrinsic worth and buy value. The margin of security transforms investing from hypothesis right into a mathematical train with favorable odds, offering draw back safety whereas sustaining upside potential.
Conclusion
Warren Buffett’s extraordinary wealth outcomes from persistently making use of these mathematical ideas to funding choices over a long time. These guidelines exhibit that profitable investing requires quantitative evaluation, probabilistic considering, and mathematical self-discipline fairly than advanced formulation or market timing.
The ability lies not within the sophistication of the arithmetic, however within the constant utility of easy, elementary ideas. By understanding and making use of these mathematical ideas, traders can construct wealth by means of the identical systematic strategy that created one among historical past’s biggest fortunes. Success comes from mathematical self-discipline, endurance, and the compounding impact of sound choices made persistently over time.